목차
안녕하세요! 생각하는 힘, 바로 논리학에 관심 많은 블로그 주인장입니다. 살다 보면 "그건 논리적으로 맞지 않아!"라는 말을 참 많이 듣게 되잖아요. 그런데 우리가 평소에 사용하는 '논리'라는 게 사실 크게 두 가지 방식, 바로 **연역법과 귀납법**으로 나뉜다는 사실, 알고 계셨나요? 🧐
저는 예전에 이 둘이 너무 헷갈려서 글을 읽을 때마다 '이게 연역인가, 귀납인가' 고민했던 기억이 납니다. 하지만 연역법과 귀납법의 차이를 명확하게 이해하는 순간, 세상이 다르게 보이더라고요. 오늘은 그 헷갈림을 한 방에 날려버리고, 전문적이면서도 쉽게 이 두 가지 논리 전개 방식을 파헤쳐 보겠습니다. 이 글을 끝까지 읽으시면 여러분의 논리력이 한 단계 업그레이드될 거라고 장담해요! 😊
1. 연역법 (Deduction): 진리를 향한 확실한 길
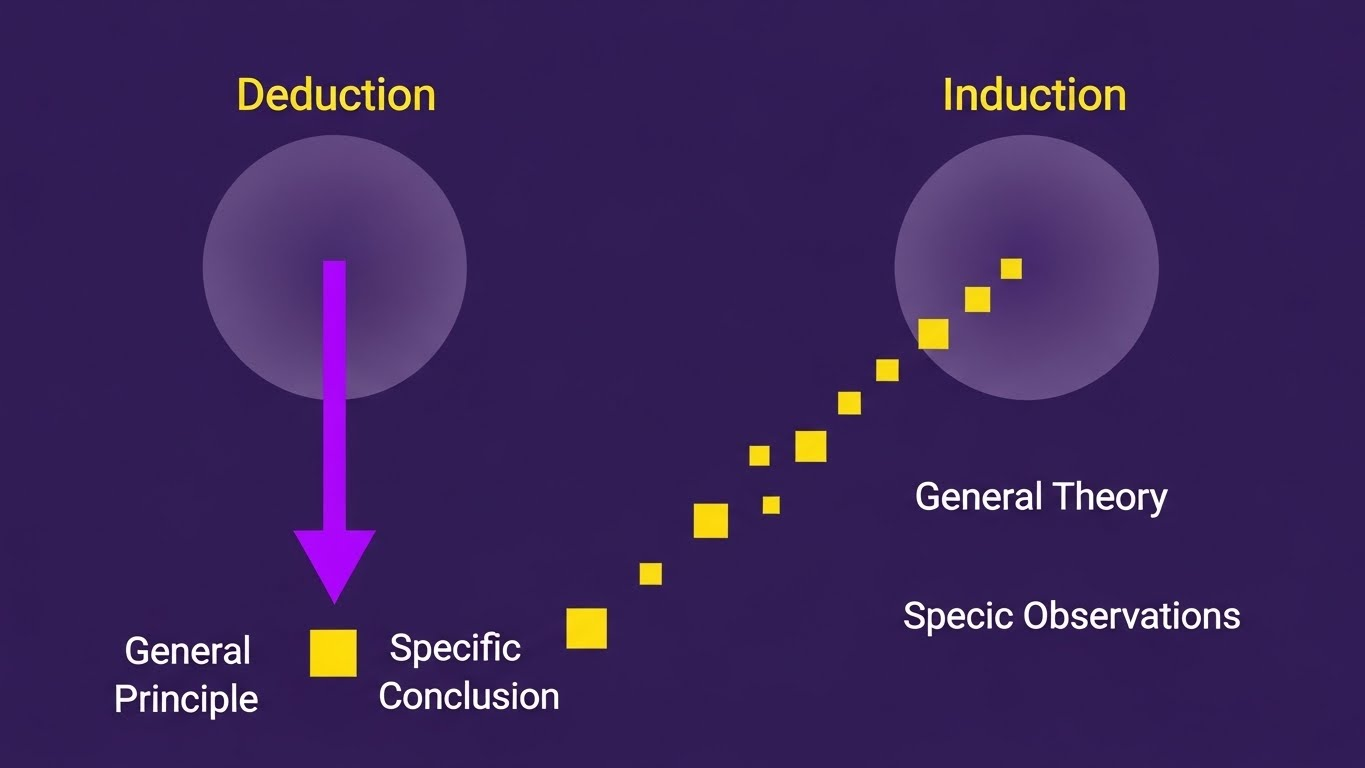
먼저 **연역법**부터 살펴봅시다. 연역법은 가장 확실하고 '진리'에 가까운 논리 전개 방식이라고 할 수 있습니다. 연역법의 핵심은 일반적인 원리나 전제로부터 구체적인 결론을 도출하는 것입니다. 즉, 전체에서 부분으로 나아가는 방식이죠.
📌 연역법의 고전적인 예시 📝
- 대전제: 모든 사람은 죽는다. (일반적 진리)
- 소전제: 소크라테스는 사람이다. (구체적 사례)
- 결론: 따라서 소크라테스는 죽는다. (필연적 결론)
여기서 중요한 포인트는, 대전제와 소전제가 **참(True)**이라면, 결론은 **필연적으로 참**일 수밖에 없다는 점입니다. 결론이 전제에 이미 내포되어 있기 때문이죠. 그래서 연역법은 수학이나 철학, 법률 등 절대적인 명제가 필요한 분야에서 아주 중요하게 사용됩니다. 이것이 바로 연역법과 귀납법의 차이 중 가장 결정적인 부분입니다.
연역법에서는 논리적 구조가 완벽하면 '타당한(Valid)' 논증이 됩니다. 여기에 전제까지 실제로 참이면 '건전한(Sound)' 논증이라고 부른답니다. 결론의 참 여부는 전제의 참에 전적으로 의존하는 것이죠.
2. 귀납법 (Induction): 새로운 지식을 창조하는 힘
다음은 **귀납법**입니다. 귀납법은 연역법과는 정반대의 방향으로 나아갑니다. 귀납법은 구체적인 관찰이나 개별적인 사례들을 모아서 일반적인 원리나 보편적인 결론을 이끌어내는 방식입니다. 부분에서 전체로 확장하는 것이죠.
📌 귀납법의 일반적인 예시 📝
- 사례 1: 제가 본 백조는 하얀색이었다.
- 사례 2: 유럽에서 관찰된 모든 백조는 하얀색이었다.
- 결론: 따라서 모든 백조는 하얀색일 것이다. (개연적 결론)
과학적 탐구, 특히 실험과 관찰을 통해 새로운 법칙을 발견하는 자연과학 분야에서는 이 **귀납법**이 필수적입니다. 우리가 알고 있는 중력의 법칙이나 진화론 같은 것도 수많은 관찰과 사례들을 통해 일반화된 귀납적 논리의 산물인 셈이죠.
다만, 귀납법은 연역법과 달리 **개연성(Probability)**을 가질 뿐, **필연성**은 없습니다. 아무리 많은 백조를 관찰해도, 다음 백조가 검은색일 가능성은 항상 존재합니다. (실제로 호주에서는 검은 백조가 발견되어 이 예시를 뒤집었죠!) 이게 바로 연역법과 귀납법의 차이에서 오는 '결론의 확실성' 문제랍니다.
귀납법은 새로운 지식을 주지만, 항상 오류의 가능성을 내포합니다. 이를 '귀납의 문제'라고 부르기도 합니다. 성급한 일반화는 잘못된 결론을 초래할 수 있으니, 충분한 사례와 객관적인 데이터가 중요합니다.
3. 연역법과 귀납법의 차이: 한눈에 비교하기
자, 이제 연역법과 귀납법의 차이점을 핵심적인 기준으로 비교해보겠습니다. 이 표 하나만 기억하셔도 두 가지 논리 전개 방식을 완벽하게 구분하실 수 있을 거예요!
| 구분 기준 | 연역법 (Deduction) | 귀납법 (Induction) |
|---|---|---|
| 논리 방향 | 일반 → 구체 (전체 → 부분) | 구체 → 일반 (부분 → 전체) |
| 결론의 확실성 | 필연적 (Necessary) | 개연적 (Probable) |
| 지식의 확장 | 없음 (기존 지식의 명료화) | 새로운 지식 확장 (New Knowledge) |
| 활용 분야 | 수학, 논리학, 법률, 증명 | 과학, 통계, 일상적 추론 |
4. 연역법과 귀납법의 실생활 활용과 조화
우리는 의식하지 못하지만, 사실 매일 연역법과 귀납법을 모두 사용하고 있습니다. 예를 들어, 아침에 '오늘은 영하 5도다 (구체적 사례) → 영하 5도에는 코트가 필요하다 (일반적 원리) → 따라서 코트를 입어야 한다 (결론)'라고 생각한다면, 이는 연역적 사고에 가깝습니다. 이미 알고 있는 사실을 적용한 것이죠.
반면에, 새로 산 커피 머신이 매번 버튼을 누를 때마다 이상한 소리를 낸다고 가정해봅시다. '첫 번째 사용 시 소음 (사례) → 두 번째 사용 시 소음 (사례) → 아마도 이 커피 머신은 소음 문제가 있을 것이다 (일반화)'라고 추론하는 것은 전형적인 **귀납적 사고**입니다. 여러 번의 관찰을 통해 잠정적인 결론을 내린 것이죠.
✨ 균형 잡힌 논리적 사고를 위한 3가지 팁
- 1. 전제 점검 (연역): 결론을 내리기 전에, 여러분의 대전제가 정말로 참인지, 믿을 만한 것인지 끊임없이 질문하세요.
- 2. 사례 확보 (귀납): 성급하게 일반화하지 마세요. 충분하고 다양한 사례를 모아야 귀납적 결론의 개연성이 높아집니다.
- 3. 비판적 시각 유지: 항상 반례(Counter-example)가 존재할 수 있음을 인정하고, 자신의 논리에 오류는 없는지 연역법과 귀납법을 번갈아 적용하며 검토해야 합니다.
글의 핵심 요약: 연역 & 귀납의 핵심 3가지
지금까지 살펴본 연역법과 귀납법의 차이를 머릿속에 확실히 정리할 수 있도록, 가장 중요한 핵심만 다시 한번 요약해 드릴게요.
- 방향성의 차이: 연역법은 일반에서 구체로, 귀납법은 구체적인 사례에서 일반적인 결론으로 향합니다.
- 결론의 성격: **연역**의 결론은 전제가 참이면 **필연적으로 참**이지만, **귀납**의 결론은 아무리 전제가 많아도 **개연적인 참**일 뿐입니다.
- 지식의 역할: **연역**은 기존 지식을 **확인하고 적용**하는 데 유용하고, **귀납**은 새로운 법칙과 이론을 **발견**하는 데 필수적입니다. 이 두 가지 사고방식의 조화가 진정한 논리적 사고를 완성합니다.
자주 묻는 질문
오늘은 우리의 생각의 틀을 이루는 연역법과 귀납법의 차이에 대해 깊이 있게 탐구해 보았습니다. 이 두 가지 논리 전개 방식은 서로 상반되지만, 세상을 이해하고 문제를 해결하는 데 있어 상호 보완적인 역할을 합니다. 이 글이 여러분의 논리적 사고를 더욱 탄탄하게 만드는 데 도움이 되었기를 바랍니다! 더 궁금한 점이 있다면 댓글로 물어봐주세요~ 언제든지 환영입니다! 😊
함께보면 도움되는 글
한국 개기일식을 볼 수 있을까? 다음 기회와 안전 관측법
목차태양이 사라지는 경이로운 순간, 개기일식! 우리 한국에서는 언제쯤 이 특별한 현상을 직접 볼 수 있을까요? 오늘은 한국에서 개기일식을 관측할 수 있는 다음 기회와 그 역사적 기록, 그리
fo.farmyse.com
태풍은 어떻게 만들어질까? 태풍 발생 원인
목차여름만 되면 왜 태풍이 찾아올까요? 매년 여름과 가을을 위협하는 강력한 자연현상, 바로 태풍! 이 무시무시한 폭풍이 대체 어디서, 어떻게 생겨나는지 궁금하지 않으신가요? 오늘은 태풍
fo.farmyse.com
이산화탄소 특징 5가지(콜라부터 지구 온난화까지)
목차숨 쉬는 순간부터 지구 온난화까지? 이산화탄소의 두 얼굴! 😮 우리가 숨을 쉴 때마다 내뱉고, 식물이 좋아하는 공기 중의 한 성분인 이산화탄소! 이름은 어렵지만 사실 우리 생활과 아주
fo.farmyse.com
'오방색 의미' : 한국의 아름다운 색
목차우리 전통 색깔, '오방색'에 숨겨진 신비한 이야기! 🌈✨ 알록달록 예쁜 색깔은 우리 주변 어디에나 있죠? 그런데 우리 조상들이 특별히 아끼고 중요하게 생각했던 다섯 가지 색깔이 있다는
fo.farmyse.com
자외선 뜻과 종류: UVA, UVB, UVC
목차햇빛을 쬐는 건 좋지만, 피부에는 조심해야 할 존재, 바로 자외선! 매일 듣는 단어지만 정확히 어떤 의미인지, 우리 몸에 어떤 영향을 미치는지 궁금하셨죠? 오늘은 자외선의 모든 것을 쉽고
fo.farmyse.com