100% 확실한 증명! 수학적 귀납법의 3단계 도미노 원리 완벽 해설

목차

 

🤔 수학적 귀납법 (Mathematical Induction)이란 무엇일까요? 일반적인 귀납법과 달리, 수학적 귀납법은 **참**임을 100% 보장하는 강력한 증명 도구입니다. 이 글에서 수학적 귀납법의 원리와 3단계 증명 과정을 쉽고 명쾌하게 설명해 드립니다.

안녕하세요! 지난번에 **연역법과 귀납법의 차이**를 살펴보면서, 일반적인 귀납법은 '개연적인 참'만을 보장한다고 말씀드렸죠. 그런데 수학에서는 이 **귀납법**이라는 이름을 달고도 **100% 확실한 참**을 증명하는, 아주 특별하고 강력한 도구가 있습니다. 바로 **수학적 귀납법**입니다! 🧐

저도 고등학교 때 수학적 귀납법을 처음 배우면서, '귀납인데 어떻게 확실한 증명이 가능하지?'라는 의문을 가졌던 기억이 나요. 하지만 그 원리를 이해하는 순간, 이 방법이 얼마나 완벽하게 논리적인지 감탄하게 되죠. 오늘은 이 수학적 귀납법의 원리를 도미노 놀이에 비유하여 쉽고 재미있게 풀어보고, 복잡한 수식이 아닌 핵심 논리에 집중하여 설명해 드리겠습니다.

100% 확실한 증명! 수학적 귀납법의 3단계 도미노 원리 완벽 해설

1. 수학적 귀납법, 그 특별한 확실성

**수학적 귀납법**은 자연수 $n$에 대한 명제 $P(n)$이 모든 자연수에 대해 성립함을 증명하는 방법입니다. 이름은 귀납법이지만, 실제로는 **연역적 논리**를 기반으로 합니다. 이 방법이 '확실한 참'을 보장하는 비결은 바로 '도미노 원리'에 있습니다.

📌 도미노 비유를 통한 원리 이해 📝

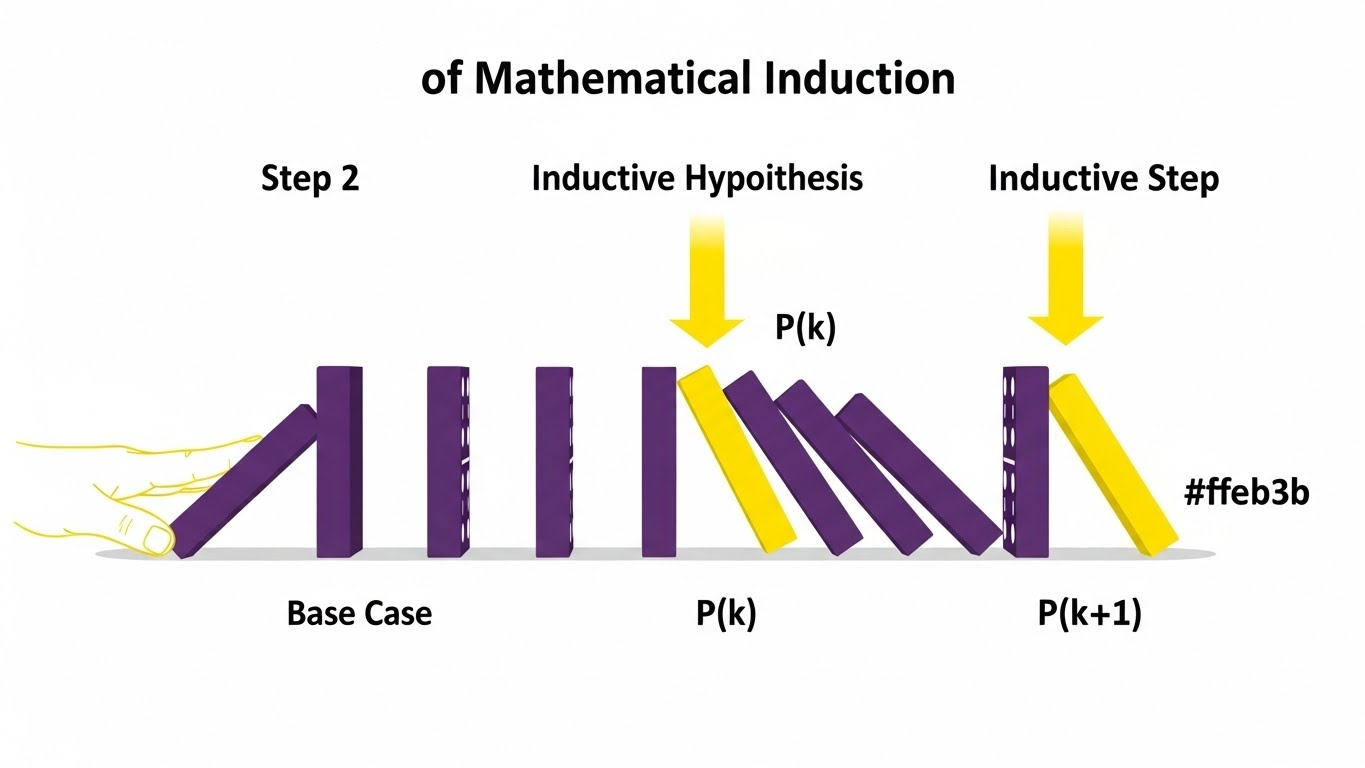
도미노를 생각해보세요. 모든 도미노를 쓰러뜨리기 위해서는 딱 두 가지 조건만 충족하면 됩니다.

• 1단계 (초기 조건): **첫 번째 도미노**가 쓰러져야 한다. ($P(1)$이 참이다)
• 2단계 (연쇄 조건): 어떤 도미노가 쓰러지면, **바로 다음 도미노도 반드시 쓰러지게** 연결되어 있어야 한다. ($P(k)$가 참이면 $P(k+1)$도 참이다)

이 두 가지 조건만 만족하면, 첫 번째 도미노를 쓰러뜨리는 순간, 두 번째, 세 번째, 그리고 **모든** 도미노(모든 자연수 $n$)가 필연적으로 쓰러지게 됩니다. 이것이 바로 수학적 귀납법이 연역법처럼 **100% 확실한 증명**을 제공하는 이유입니다. 일반적인 귀납법이 관찰되지 않은 사례를 포괄할 때 개연성만 가지는 것과 근본적으로 다른 점이죠.

💡 수학적 귀납법은 귀납이 아닌 연역이다?
수학적 귀납법은 '자연수 전체에 대해 성립하는지 확인한다'는 점에서는 일반 귀납법과 유사하지만, 그 증명 논리(도미노 원리) 자체가 전제로부터 필연적인 결론을 이끌어내는 **연역적 추론**입니다. 그래서 '수학적 연역법'이라고 불러야 한다는 주장도 있답니다.

 

2. 실전! 수학적 귀납법의 3단계 증명 공식

어떤 명제 $P(n)$을 수학적 귀납법으로 증명할 때는 다음의 세 가지 단계를 순서대로 밟아야 합니다. 이 단계가 바로 도미노 원리를 수학적으로 구현하는 핵심입니다.

1. 1단계: 기본 단계 (Base Case) 🌟
   명제 $P(n)$이 **최초의 자연수** (대부분 $n=1$ 또는 문제에서 제시된 초기값)에 대해 성립함을 직접 증명합니다. 이것은 **'첫 번째 도미노를 쓰러뜨리는'** 단계에 해당합니다. 이 단계가 없으면 증명은 시작조차 할 수 없습니다.
2. 2단계: 귀납적 가설 (Inductive Hypothesis) 🤝
   임의의 자연수 $k$에 대하여, 명제 $P(k)$가 **참이라고 가정**합니다. 이 단계는 **'도미노가 쓰러지는 중이라고 가정'**하는 것입니다. 이 가정이 다음 단계를 증명하기 위한 발판이 됩니다.
   가정: $P(k)$는 참이다.
3. 3단계: 귀납적 단계 (Inductive Step) 🔗
   2단계의 가정($P(k)$가 참)을 이용하여, 명제 $P(k+1)$이 **참임을 증명**합니다. 이 단계는 **'k번째 도미노가 쓰러지면, k+1번째 도미노도 반드시 쓰러진다'**는 연결 고리를 수학적으로 완성하는 것입니다. 이 연결 고리만 성공적으로 증명하면, 수학적 귀납법은 완성됩니다.
   증명 목표: $P(k)$를 이용해 $P(k+1)$이 참임을 보인다.

 

3. 수학적 귀납법은 언제 사용될까요?

수학적 귀납법은 주로 '자연수에 대해 성립하는' 다음과 같은 명제들을 증명할 때 사용됩니다.

📝 수학적 귀납법의 대표적인 활용 예

• 수열의 합 공식 증명: $1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2}$ 와 같은 합 공식이 모든 자연수 $n$에 대해 참임을 증명할 때.
• 부등식 증명: 특정 부등식(예: 베르누이 부등식)이 모든 자연수 $n \ge n_0$에 대해 성립함을 증명할 때.
• 배수 관계 증명: $3^n - 1$이 항상 짝수임을 증명하는 것과 같이, 어떤 식이 특정 수의 배수임을 증명할 때.
• 재귀적 정의: 컴퓨터 과학에서 알고리즘이나 자료 구조의 정확성을 증명할 때 사용되는 강력한 기법입니다.

⚠️ 1단계 (Base Case)를 빼먹지 마세요!
2단계와 3단계가 아무리 완벽해도, 1단계($P(1)$) 증명을 빠뜨리면 증명은 무너집니다. **첫 번째 도미노**를 쓰러뜨리지 않으면 아무리 연결 고리가 잘 되어 있어도 모두 쓰러지지 않는 것과 같습니다. 이는 수학적 귀납법을 사용할 때 가장 흔하게 저지르는 실수입니다.

 

자주 묻는 질문: 수학적 귀납법 Q&A

Q: 수학적 귀납법은 모든 수학적 명제를 증명할 수 있나요?

A: 아닙니다. 수학적 귀납법은 오직 자연수 $n$에 대해 정의된 명제 $P(n)$에 대해서만 사용할 수 있습니다. 실수나 복소수에 대한 명제, 또는 자연수가 아닌 대상에 대한 명제에는 사용할 수 없습니다.

Q: $P(k)$가 참이라고 '가정'하는 것이 정말 논리적으로 문제가 없나요?

A: 네, 논리적으로 완벽합니다. 수학적 귀납법은 $P(k)$가 '참일 때' $P(k+1)$도 참임을 보이는 조건부 증명입니다. 1단계에서 $P(1)$이 참임을 보였으므로, $P(1) \implies P(2)$, $P(2) \implies P(3)$, $\cdots$ 의 연쇄적인 참이 보장됩니다. 이것이 바로 공리(페아노 공리계)에 기반한 수학적 귀납법의 힘입니다.

오늘은 일반 귀납법과는 차원이 다른, 절대적인 확실성을 제공하는 수학적 귀납법에 대해 깊이 있게 알아보았습니다. 이 증명 방법은 단순한 암기가 아닌, 논리적 연결 고리를 이해하는 것이 핵심입니다. 도미노 원리만 잘 기억하신다면, 앞으로 어떤 $P(n)$ 명제도 자신 있게 증명하실 수 있을 거예요! 궁금한 점은 언제든지 댓글로 남겨주세요~ 😊

 

함께보면 도움되는 글

한국 개기일식을 볼 수 있을까? 다음 기회와 안전 관측법

태풍은 어떻게 만들어질까? 태풍 발생 원인

이산화탄소 특징 5가지(콜라부터 지구 온난화까지)

'오방색 의미' : 한국의 아름다운 색

자외선 뜻과 종류: UVA, UVB, UVC